C - 積み上げパズル
Editorial
 /
/ 
高橋君はある日、以下のようなゲームで遊ぶことにしました。
m 色のブロックが n 個、1 つずつ順番に落ちてきます。
1 つ落ちてくるたびに、高橋君は落ちてきたそのブロックを取って山に積むか、積まずに捨てるか選べます。
ブロックを積む山は 1 つで、ブロックは必ず山の一番上に積まないといけません。
全てのブロックが落ちきった後、出来た山は以下のように評価されます。
入力は以下の形式で標準入力から与えられる。
評価で得ることのできる得点の最大値を標準出力に 1 行で出力せよ。
なお、最後には改行を出力せよ。
 /
/ 
Time Limit: 2 sec / Memory Limit: 64 MB
問題文
m 色のブロックが n 個、1 つずつ順番に落ちてきます。
1 つ落ちてくるたびに、高橋君は落ちてきたそのブロックを取って山に積むか、積まずに捨てるか選べます。
ブロックを積む山は 1 つで、ブロックは必ず山の一番上に積まないといけません。
全てのブロックが落ちきった後、出来た山は以下のように評価されます。
- 色ボーナス:色ごとに決められた得点が、山に含まれている個数分与えられます。
- コンボボーナス:同じ色のブロックが x 個続いて積まれている場合、コンボボーナス配点 Y に応じて Y×(x-1) 点が与えられます。
- 全色ボーナス:山の中に m 色のブロックがそれぞれ 1 個以上含まれていると Z 点が与えられます。
入力
n m Y Z c_1 p_1 c_2 p_2 : : c_m p_m b_1b_2 ‥‥ b_n
- 1 行目に n, m, Y, Z が半角スペースで区切られて与えられる。
- n はブロックの個数で 1≦n≦5,000 を満たす。
- m はブロックの色の総数で 1≦m≦10 を満たす。
- Y はコンボボーナス配点で -100≦Y≦100 を満たす。
- Z は全色ボーナス配点で -10,000≦Z≦10,000 を満たす。
- n, m, Y, Z は全て整数である。
- 2 行目からの m+1 行目までの m 行で色ボーナスの配点がそれぞれ与えられる。
- c_i は i(1≦i≦m) 番目に与えられるブロックの色である。
- p_i は c_i に対する色ボーナスの配点である。
- c_i は英大文字(
A-Z)、p_i は -100≦p_i≦100 を満たす。 - 配点は重複して与えられない(x≠y ならば c_x≠c_y)
- m+2 行目には落ちてくるブロックの順序を表す長さ n の文字列が与えられる。
- b_j は j(1≦j≦n) 番目に落ちてくるブロックの色を表している。
- b_j は c_1,c_2,...,c_m のいずれかである。
出力
なお、最後には改行を出力せよ。
入力例 1
5 3 3 5 R 1 G 1 B 1 RGBRR
出力例 1
13
- 全てのブロックを山に積むと、
- 色ボーナス:どの色も配点が 1 点なので、1 点 × 5 個 = 5点
- コンボボ−ナス:Rが 2 個連続しているので、3×(2-1)=3 点
- 全色ボーナス:全ての色が 1 つ以上山に積まれているので、5 点
- いずれかのブロックを捨てるとこの点数よりも低くなるので、答えは 13 点です。
入力例 2
3 3 3 5 R 1 G 3 B 2 RBR
出力例 2
5
- 全てのブロックを山に積むと、
- 色ボーナス:1 点 ×2 個 +2 点 ×1 個 =4 点
- 連続していないのでコンボボーナス、Gが含まれていないので全色ボーナスはそれぞれ 0 点
- しかし、Bを捨ててRRを山に積むと、
- 色ボーナス:1 点 ×2 個 =2 点
- コンボボーナス:3×(2-1)=3 点
入力例 3
8 3 5 3 R 1 G 1 B 1 RRGRRBRR
出力例 3
31
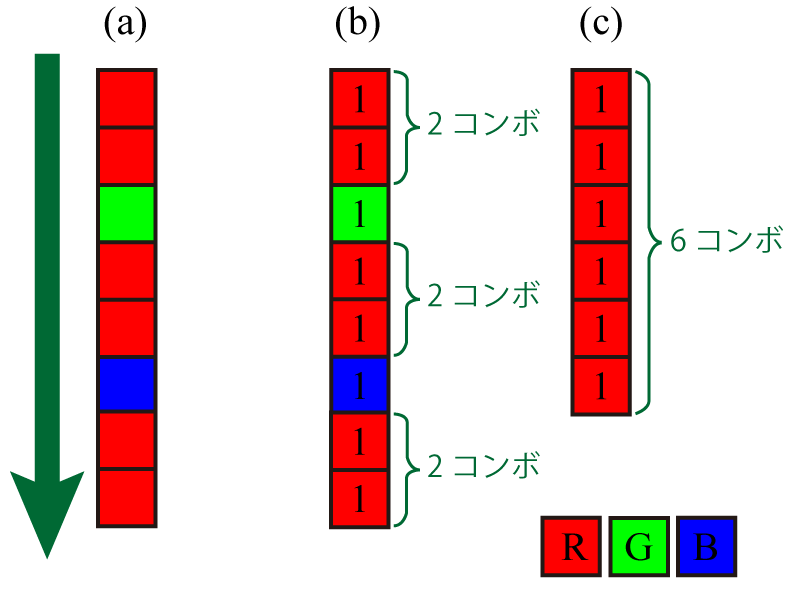
- 図 (a) のように順に 8 個のブロックが落ちてきます。
- ブロックを全部山に積むと、図 (b) のように、2 個のコンボが 3 組できます。
- また、全色ボーナスもつくので、1 点 × 8 個 + 5 点 × (2-1) × 3 組 + 3 点 = 26 点です。
- しかし、図 (c) のようにRのみを山に積むと、1 点 × 6 個 + 5 点 × (6-1) + 0 点 = 31 点になります。
- Rだけ山に積むとき最高得点となり、31 が答えです。

入力例 4
8 3 5 3 R 1 G 100 B 1 RRGRRBRR
出力例 4
126
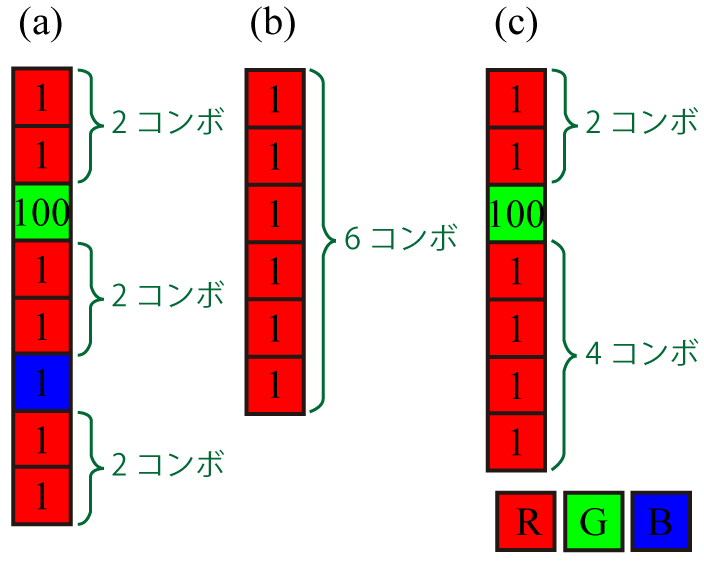
- 全部積んだ場合(図 (a)):107 点 + 5 点 × (2-1) × 3 組 + 3 点 = 125 点
- Rのみを積んだ場合(図 (b)):6 点 + 5 点 × (6-1) + 0 点 = 31 点
- B以外を積んだ場合(図 (c)):106 点 + 5 点 × \{(2-1) + (4-1)\} + 0 点 = 126 点
- したがって、最高得点は 126 点です。
